비전공자를 위한 알고리즘 강의 1부 - 시작 및 BigO 표기법

본 블로그 글은 비전공자를 위한 알고리즘 강의이며 취준생인 여자친구를 위해 작성하므로 정성스레 적을 예정입니다.

본인도 비전공자 출신이며 현재 대기업에서 일하고 있습니다.

비전공자로 공부하면서 힘들었던 점들과 노하우를 공유할 예정이니 하나하나 놓치지 말고 꼼꼼히 읽어주시면 감사하겠습니다.

0. 알고리즘 시험에서 알아야 할 키워드

다음은 알고리즘 시험을 공부할 때 꼭 알아야 하는 키워드 입니다.

프로그래밍에서 1초가 걸리는 알고리즘은 어떤 알고리즘인가
BigO 표기법 - 나의 알고리즘이 대략적으로 몇 초가 걸릴지 예측하는 방법
자료구조 - 큐, 스택, 덱(deque), 집합(set), 사전형(map), 우선순위큐(heap)

정렬 - 커스텀 정렬 만들기, 우선순위 큐 커스텀 정렬 만들기

완전탐색 - DFS, BFS
다이나믹 프로그래밍
문자열 다루기 - 자르기, 붙이기, 특정부분 단어 변환, 소문자 대문자 변환 등

다익스트라 알고리즘


파란색으로 칠한 자료구조는 사용법을 꼭 알아놔야 문제를 쉽게 풀 수 있습니다.
특히 우선순위큐 사용법은 반드시 익혀놔야 시간초과 문제를 쉽게 해결 할 수 있으며
커스텀 정렬, 우선순위큐 커스텀 정렬 만드는법도 반드시 외워놔야 합니다.


빨간색으로 칠한 DFS, BFS는 기초중에 기초인 알고리즘 입니다.
모 대기업 s사 같은경우는 저 문제유형만 출시하는 편입니다.

다익스트라 알고리즘은 외워두면 다른 알고리즘 풀 때 응용이 가능하니 필히 외워두시기 바랍니다.

1. 알고리즘 시험은 어떻게 나오는가

https://www.acmicpc.net/problem/6198

6198번: 옥상 정원 꾸미기

위 링크에서 나온 문제가 대표적인 예시입니다.

1. 문제상황을 주고
2. 인풋을 주고
3. 받은 인풋을 토대로 알고리즘을 작성하여 답을 출력하면 됩니다.


풀려고는 하지 마시고 한번 쭈욱 읽어보시길 바랍니다.

ㅡㅡㅡㅡㅡㅡㅡㅡㅡㅡㅡㅡㅡㅡㅡㅡㅡㅡㅡㅡㅡㅡㅡㅡㅡㅡㅡㅡㅡㅡㅡㅡㅡㅡㅡㅡㅡ

도시에는 N개의 빌딩이 있다.

빌딩 관리인들은 매우 성실 하기 때문에, 다른 빌딩의 옥상 정원을 벤치마킹 하고 싶어한다.

i번째 빌딩의 키가 hi이고, 모든 빌딩은 일렬로 서 있고 오른쪽으로만 볼 수 있다.

i번째 빌딩 관리인이 볼 수 있는 다른 빌딩의 옥상 정원은 i+1, i+2, .... , N이다.

그런데 자신이 위치한 빌딩보다 높거나 같은 빌딩이 있으면 그 다음에 있는 모든 빌딩의 옥상은 보지 못한다.

예) N=6, H = {10, 3, 7, 4, 12, 2}인 경우

             = 
 =           = 
 =     -     = 
 =     =     =        -> 관리인이 보는 방향
 =  -  =  =  =   
 =  =  =  =  =  = 
10  3  7  4  12 2     -> 빌딩의 높이
[1][2][3][4][5][6]    -> 빌딩의 번호

• 1번 관리인은 2, 3, 4번 빌딩의 옥상을 확인할 수 있다.
• 2번 관리인은 다른 빌딩의 옥상을 확인할 수 없다.
• 3번 관리인은 4번 빌딩의 옥상을 확인할 수 있다.
• 4번 관리인은 다른 빌딩의 옥상을 확인할 수 없다.
• 5번 관리인은 6번 빌딩의 옥상을 확인할 수 있다.
• 6번 관리인은 마지막이므로 다른 빌딩의 옥상을 확인할 수 없다.

따라서, 관리인들이 옥상정원을 확인할 수 있는 총 수는 3 + 0 + 1 + 0 + 1 + 0 = 5이다.

입력

• 첫 번째 줄에 빌딩의 개수 N이 입력된다.(1 ≤ N ≤ 80,000)
• 두 번째 줄 부터 N+1번째 줄까지 각 빌딩의 높이가 hi 입력된다. (1 ≤ hi ≤ 1,000,000,000)

 

출력

• 각 관리인들이 벤치마킹이 가능한 빌딩의 수의 합을 출력한다.

예제 입력 1 복사

6
10
3
7
4
12
2

예제 출력 1 복사

5

ㅡㅡㅡㅡㅡㅡㅡㅡㅡㅡㅡㅡㅡㅡㅡㅡㅡㅡㅡㅡㅡㅡㅡㅡㅡㅡㅡㅡㅡㅡㅡㅡㅡㅡㅡㅡㅡㅡㅡㅡ



자 어떠신가요? 읽어보시고 쉽게 아이디어 올려서 푸실 수 있으신가요? 막막하지요?
아이디어가 떠오르셨다면 천재시니 이 글을 더이상 읽지 않으셔도 됩니다.

2. 공부는 어떻게 하나요?

문제를 보시니 막막하지요. 나는 수학머리가 없어서 저런거 어떻게 풀지 아마 이런 생각이 드실겁니다.
하지만 걱정마세요.
필자는 수능때 수리 가형 만점을 받았던 사람인데 저 또한 문제를 보고 어떻게 풀지하고 똑같이 막막했습니다.

처음 보고 막막한건 당연하단 소리입니다.


결론부터 말하면 알고리즘 문제는 수학이 아닙니다.

일단 수학에서 사용하던 풀이법을 컴퓨터에 그대로 적용 할 수 없습니다.

가령 우리가 인수분해를 한다고 칩시다.

위 그림은 아주 쉬운 인수분해 예제입니다. 위 문제를 보고

상수가 2인데 이게 -1, -2 를 곱하면 나오니 위 그림처럼 적고 x자로 곱하면 답은 (x-2)(x-1) 이네!

라고 쉽게 나오지만 컴퓨터로 위 방법을 적용할수 있나요? 쉽지 않습니다.



문제 유형이 정해져 있고 달달 외우시면 충분히 해결 가능합니다. 이게 핵심

아까 위에 백준에서 나온 문제는 stack을 이용하면 쉽게 해결되는 문제입니다.


여러분이 알고리즘 문제를 보면 외워놓은 정해진 유형 내에서 문제와 계속 매칭하고 맞는게 있으면 그걸 그대로 풀어내면 됩니다.

"이 문제는 큐? 맵? 우선순위큐를 이용하는 문제인가? 아니면 완전탐색인가? 아니면 다이나믹 프로그래밍? 아 스택을 이용하는 문제군! 스택쓰면 되겠다!"

문제를 풀 때 위와같은 생각 패턴으로 푸시면 되는겁니다.

세계 정보 올림피아드 출전 선수들 영상보면 똑같이 영어로 저렇게 얘기합니다.

"Is it queue? or stack? Oh It seems that dp(dynamic programing)!"



아래 내용들을 반드시 기억해 줍니다

• 막막한건 당연한겁니다. 걱정하지마세요.
• 공부를 할 때 설명을 보면 이해도 안되는것도 당연한 겁니다.
• 이해 안되는거 계속해서 반복해서 보세요. 그럼 이해 됩니다.
• 기초중에 기초인 BFS, DFS, 그리고 다익스트라 알고리즘은 달달 외워둡니다.
• 알고리즘 공부라는게 처음하면 생각보다 시간이 걸립니다. 적어도 2달은 되어야 눈에 보이기 시작합니다.

 

반응형

 

3. 언어는 무엇으로 하면 좋나요?

c++, java, python 이 세개를 추천드립니다. 유저들이 많고 자료가 많으니깐요.


특히 python은 알고리즘 풀이에 다른 언어에 비해 약간의 이득이 있습니다. 똑같은 문제라도 훨씬 쉽게 풀리죠.


나는 c밖에 안배웠는데 c는 안되나요? 하시는 분들이 있습니다.


이런분들도 반드시 c++로 풀어야 합니다. 단 객체지향까지 파고들 필요가 없습니다.
vector, queue, priority_queue, stack, map, set 이런 STL Container 사용법만 익혀두시면 됩니다.
순수 c로만 푼다면 상당히 고달프니 stl 사용법을 꼭 익히도록 합시다

4. 컴퓨터에서 1초가 걸리는 알고리즘

자 본론으로 넘어갑시다.

대부분 알고리즘 문제들은 시간 제한이 있으며 대부분 1초 입니다.

그럼 언제 알고리즘이 1초가 걸리는지 알아야 겠지요?



결론부터 말씀드립니다.

현세대 cpu는 GHz로 동작합니다. 고로 여러분의 알고리즘이 GHz만큼 동작하면 1초가 걸립니다.

 

그리고 코드 한줄당 1hz를 소비한다고 생각하면 됩니다.

G, Giga라는 단위는 10^9 입니다. 여러분의 코드가 10^9 이상 돈다면 여러분은 시간초과로 시험에서 탈락하게 됩니다.


고로 알고리즘을 짜실 때 10^8 이내로 들어오도록 하시고 대부분 10^6으로 짯다면 맞췄다고 생각하시면 됩니다.




가령 예시를 들면 다음과 같은 문제가 있습니다.

인풋 N을 입력받고 N+1을 출력하세요

아래처럼 풀면 합격입니다.

int N = getInput();
print(N+1);

허나 알고리즘을 아래처럼 작성했다고 가정해 봅시다.

int N = getInput();
int answer = 1;
for(int i=0; i<N; i++){
	answer+=1;
}
print(answer);

N이 작은값이면 문제가 없습니다. 허나 N이 10^9 이라면?

1초가 더 걸려서 문제푸는데 실패 할 수 있습니다.

중요한 내용이니 반드시 숙지하도록 합시다.

 

4. BigO 표기법

BigO 표기법이란 내가 작성한 알고리즘이 대략적으로 얼마나 걸리는지 계산하는 방법입니다

아래가 대표적인 계산 방법입니다.

• 나의 알고리즘이 상수함수 형태를 띈다 => O(1)
• 나의 알고리즘이 일차함수 형태를 띈다 => O(N)
• 나의 알고리즘이 로그함수 형태를 띈다 => O(logN)
• 나의 알고리즘이 일차함수x로그함수 형태를 띈다 => O(N*logN)
• 나의 알고리즘이 이차함수 형태를 띈다 => O(N^2)
• 나의 알고리즘이 팩토리얼 형태를 띈다 => O(N!)

무슨말인지 감이 안잡히시지요? 다시 예제를 통해 한번 봅시다.

인풋 N을 입력받고 N+1을 출력하세요

 

1. O(1) 알고리즘

위 문제의 해결법으로 아래와 같이 해결했다고 합시다

int N = getInput(); 
print(N+1);

위 알고리즘은 N값이 무엇이든 간에 코드 한줄이면 답이 나옵니다.
N값에 상관없이 항상 같은 코드로 해결이 되므로 상수함수로 생각 할 수 있습니다.

상수함수의 알고리즘은 O(1) 이라고 표현합니다.

2. O(N) 알고리즘

int N = getInput(); 
int answer = 1; 
for(int i=0; i<N; i++){ 
    answer+=1; 
} 
print(answer);

위 예제는 인풋을 받고 for문을 N번 돌립니다. 일차함수 형태를 띄지요
이럴때 위 알고리즘의 BigO 표기법은 O(N) 입니다.

만약 일차함수가 2N+3 뭐 이런형태면 어떻게 표기할까요?
상관없습니다 일차함수면 그냥 O(N) 이라고 표기하면 됩니다.

빅O 표기법은 다음과 같은 특징을 가진것을 기억하세요

BigO 표기법은 Rough(대충)하게 계산하는게 목적이므로 함수의 기울기나 계수는 무시한다
영향력 없는 부분은 무시한다

2N+3 의 일차함수인게 중요하지 2N이냐 10이냐 중요하지 않습니다. 무시합시다.
그리고 +3 부분은 N값이 커질수록 영향력이 미미합니다.

고로 위 알고리즘은 O(N) 이 됩니다.

3. O(N^2) 알고리즘

int N = getInput();
int answer = 1;
for(int i=0; i<N; i++){
	for(int j=0;j<N;j++){
    	answer+=1;
    }
    answer-=N;
}
print(answer+1);

위 알고리즘은 for문을 두번 돌리므로 O(N^2)형태를 띕니다.

O(N^2) 형태는 몹시 중요한 형태입니다.

N값이 10^5을 넘어가면 무조건 시간초과가 걸리는 알고리즘이기 때문이죠!

만약 여러분이 알고리즘을 짰는데 N값이 10^5이상이고 O(N^2) 띄고 있다면 문제 잘못풀었다고 생각하면 됩니다.

그리고 알고리즘을 최적화 해서 어떻게든 O(NlogN), 보통 이게 대표적입니다. 혹은 그보다 짧게 걸리는 O(N), O(logN), O(1) 형태로 바꾸셔야 합니다.

기억하세요. O(N^2)으로 시간초과 났다? 그럼 O(NlogN)혹은 그 보다 짧은 알고리즘으로 바꿔야 합니다.

자 아까 위에 배웠던 BigO 표기법의 특징을 이용하여 2N^2+3N+4 의 알고리즘은 BigO 표기법으로 어떻게 표기할까요?

답은 O(N^2) 입니다.


2N^2의 2는 중요하지 않습니다. 이차함수인게 중요하지. 무시합니다.
3N은 N값이 커지면 2N^2에 비해 영향력이 미미합니다. 무시합시다
4도 N값이 커지면 영향력이 없습니다 무시합시다.

4. O(logN) 알고리즘

비전공자분들이 아마 가장 힘들어하시는 형태가 아마 이 logN 형태가 아닐까 싶습니다.
어떻게 하면 알고리즘이 logN이 나올까요?



간단한 예시를 들어보겠습니다.


여러분 대학교 신입생때 업앤다운 게임 기억나시나요?
선배들이 나이을 맞춰보라 하고 숫자를 부르고
만약 틀릴경우 내가 부른 숫자에서 위인지 아래인지 말해주고 술 한잔 마시는 게임이죠.


여기서 저는 O(logN)인 함수인 이분탐색 알고리즘이라는 것을 적용해 보겠습니다.

이분 탐색이란 어떤 정렬된 배열에 원하는 숫자를 찾을때 배열 가운데 숫자를 선택하고
만약 틀리면 나머지 숫자를 버리고 다시 위 과정을 똑같이 반복하는 것입니다.



자 선배가 본인 나이가 1살 이상 30살 이하라고 알려주었습니다.
그리고 선배의 나이는 26살이라고 가정해 봅시다.


신입생A와 신입생B가 있습니다.

신입생A는 O(N) 알고리즘을 이용하여 선배의 나이를 맞출겁니다.
신입생B는 이분탐색을 이용하여 선배의 나이를 맞출겁니다.


신입생A: 1살, 2살, 3살, 4살, ..... 26살!
저런, 신입생A는 정답을 맞출 때 까지 술을 25번이나 마셨군요 ㅠㅠ


신입생B: 15살이요(1~30의 중간)
선배 : UP! 한잔 마시세요.
신앱생B: 23살이요!(16~30 의 중간)
선배 : UP! 한잔 마시세요!
신입생B: 27살이요!(24~30의 중간)
선배: DOWN! 한잔 마시세요!
신입생B: 25살이요!(24~26의 중간)
선배: UP! 한잔마시세요
신입생B: 26살이요!
선배: 정답!


신입생B는 이분탐색을 이용하여 5번만에 맞추었습니다!

바로 위 이분탐색이라는 알고리즘이 대표적인 logN 의 알고리즘입니다.
2로 나누기를계속한다? 그럼 log네! 라고 생각해도 무방하십니다.
그리고 이 로그는 밑이 2인 로그이지요. 보통 컴퓨터 알고리즘에서 log은 밑이 2인 알고리즘을 뜻합니다.


자 정리해서 다시한번 비교해 볼 까요?

신입생A의 알고리즘 O(N)을 이용해서 선배의 나이를 맞춘다면 위 케이스에서 최악에 케이스로 30번 시도끝에 맞출 수 있습니다.

하지만 신입생B의 경우 O(logN)을 이용하면 밑이2인 log30 =4.xxxx 이니 최소 5번만에 정답을 맞출 수 있습니다.




만약 N이 한 10억이면 얼마나 걸릴까요?

신입생A의 알고리즘은 정답을 맞출때 최대 1초가 걸릴 수 있습니다.
신입생B의 경우 밑이2인 log1000000000 = 29.xxx 이기에 나노세컨드 단위로 계산됩니다.

엄청나게 차이나요?

만약 O(N^2)으로 풀었다면 300년이나 걸립니다.
알고리즘 하나 차이로 300년이나 차이 날 수 있습니다. 엄청나지요.
이게 바로 여러분이 알고리즘을 배워야할 이유 입니다!

(라고 써놨지만 사실 취준때 말고 별 쓸일이....)

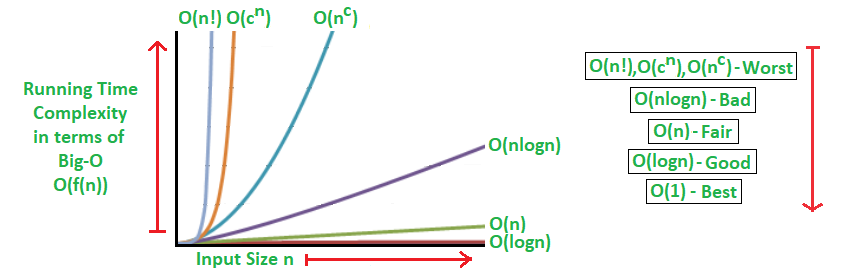
마무리로 BigO 표기법에 따른 알고리즘 성능을 나타내는 그래프를 공유하고 마치도록 하겠습니다


다음시간에는 자료구조가 왜 필요한지에 대해서 알아보겠습니다!

https://media.geeksforgeeks.org/wp-content/cdn-uploads/mypic.png